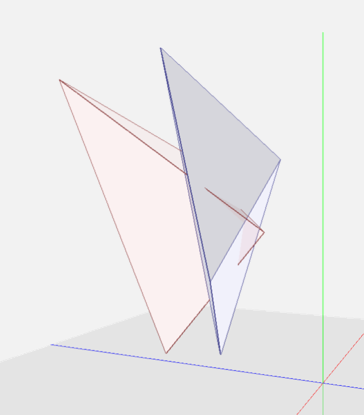
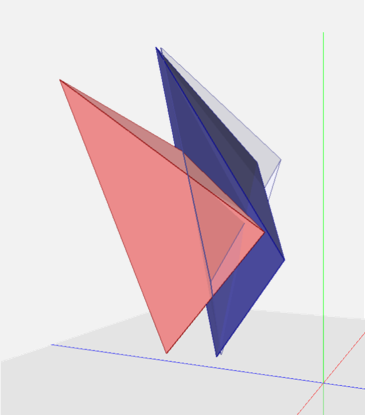
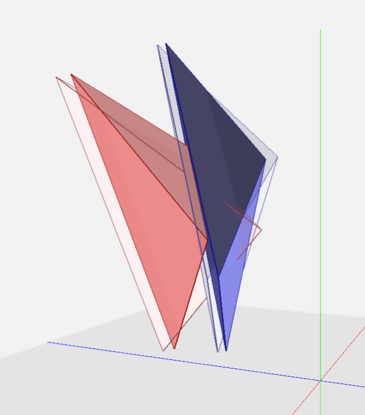
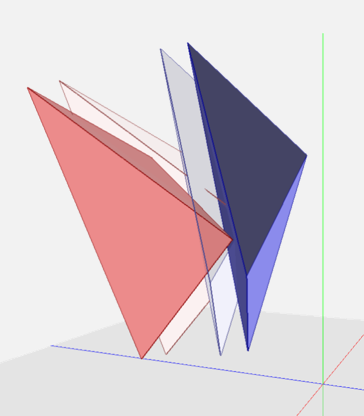
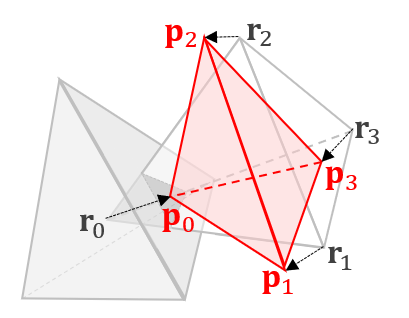
We propose a novel penetration metric, called deformable penetration depth PDd, to define a measure of inter-penetration between two linearly deforming tetrahedra using the object norm σ. Given an intersecting pair of linearly deforming tetrahedra, T1, T2, with the corresponding, initial configurations q0T1, q0T2 , their PDd is:
where C ∈ R24 is the contact (configuration) space imposed by T1, T2. Note that the proposed PDd is a generalization of the classical rigid (or translational) penetration depth.

(a) Rest State q0
(b) Deformed State q1
Fig. 1. Linear deformation of a tetrahedron to resolve inter-penetration from the rest q0 to deformed configuration q1.
As illustrated in Fig. 5, every result using PDd resolves penetration.The average performance results of each case are shown in Table 1. The running time for the static/deformable case is slightly faster than the deformable/deformable case since a fewer number of variables are required to optimize. The accelerated deformable/deformable case can be calculated in 1.07 milliseconds on average.
|
STAT/DEF |
DEF/DEF |
DEF/DEF(ACCEL.) |
|
Performance
|
32.26 ms |
46.29 ms |
1.07 ms |
|
PDd/PD
|
43.59% |
27.94% |
29.39% |
Table 1. Performance statistics
To the best of our knowledge, there are no penetration depth algorithms for deformable models available to guarantee full separation as a result (i.e. penetration metric with a tight upper bound). All the known penetration depth algorithms for deformable models provide only a lower bound, which does not guarantee full penetration resolution. Thus, it is unfair to compare our algorithms against existing algorithms for deformables and instead we compare our algorithms with rigid PD, which can be considered as an upper bound for deformable penetration depth.
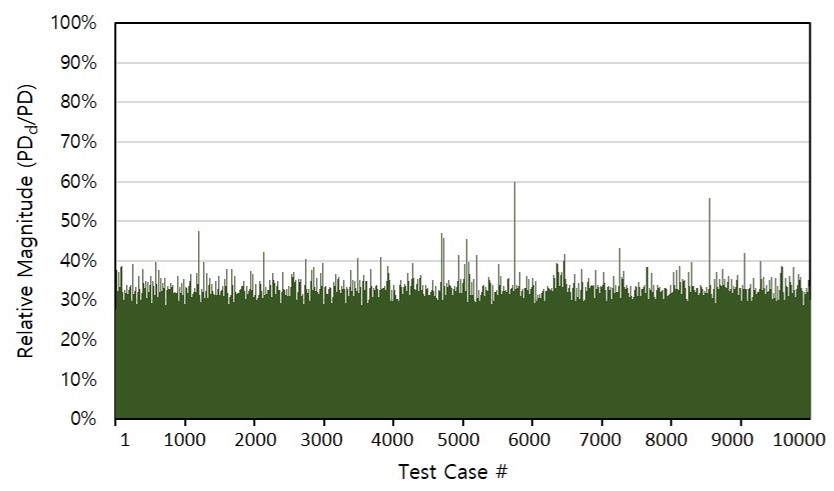
In this case, in order to show the tightness of the metric upper bounds, we calculate the relative magnitude of PDd with respect to rigid penetration depth PD. Fig. 6 shows that the magnitude of PDd is less than 1 3 of that of the rigid case most times. This means that PDd provides a much tighter deformation metric than using the rigid penetration depth.
Fig. 6. Relative magnitude of PDd over rigid penetration depth PD in 104 times of penetration resolution tests of randomly intersecting tetrahedron pairs. The average magnitude is 27.94%
Contact
Ewha Graphics Lab
Department of Computer Science & Engineering, Ewha Womans University
52, Ewhayeodae-gil, Seodaemun-gu, Seoul, Korea,
03760
+82-2-3277-6798
Jisu Kim, cwyh5526@ewhain.net
Young J. Kim, kimy@ewha.ac.kr