IEEE RA-L 2021
IEEE ICRA 2020
Abstracts
IEEE RA-L 2021, extension with complexity reducing strategy using trajectory planning:
One challenge of legged locomotion on uneven terrains is to deal with both the discrete problem of selecting a contact surface for each footstep and the continuous problem of placing each footstep on the selected surface. Consequently, footstep planning can be addressed with a Mixed Integer Program (MIP), an elegant but computationally-demanding method, which can make it unsuitable for online planning. We reformulate the MIP into a cardinality problem, then approximate it as a computationally efficient l1-norm minimisation, called SL1M. Moreover, we improve the performance and convergence of SL1M by combining it with a sampling-based root trajectory planner to prune irrelevant surface candidates.
Our tests on the humanoid Talos in four representative scenarios show that SL1M always converges faster than MIP. For scenarios when the combinatorial complexity is small (<10 surfaces per step), SL1M converges at least two times faster than MIP with no need for pruning. In more complex cases, SL1M converges up to 100 times faster than MIP with the help of pruning. Moreover, pruning can also improve the MIP computation time. The versatility of the framework is shown with additional tests on the quadruped robot ANYmal.
IEEE ICRA 2020, primary version:
One of the main challenges of planning legged locomotion in complex environments is the combinatorial contact selection problem. Recent contributions propose to use integer variables to represent which contact surface is selected, and then to rely on modern mixed-integer (MI) optimization solvers to handle this combinatorial issue. To reduce the computational cost of MI, we exploit the sparsity properties of L1 norm minimization techniques to relax the contact planning problem into a feasibility linear program. Our approach accounts for kinematic reachability of the center of mass (COM) and of the contact effectors. We ensure the existence of a quasi-static COM trajectory by restricting our plan to quasi-flat contacts. For planning 10 steps with less than 10 potential contact surfaces for each phase, our approach is 50 to 100 times faster that its MI counterpart, which suggests potential applications for online contact re-planning. The method is demonstrated in simulation with the humanoid robots HRP-2 and Talos over various scenarios.
Experimental Results
The results show the dynamically consistent whole-body motions generated using an open-source whole-body motion generation framework based on our contact plans.
Humanoid, Talos (X3 speed)

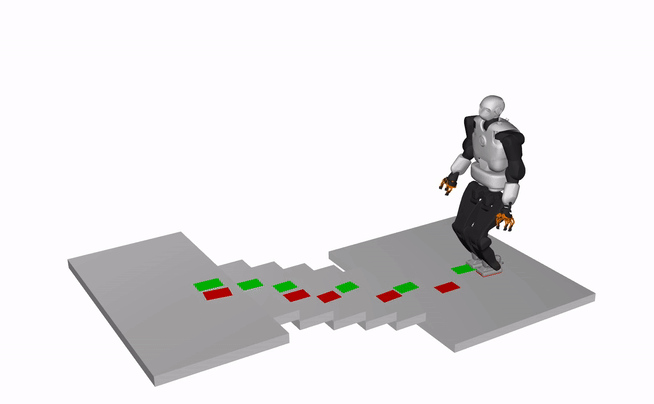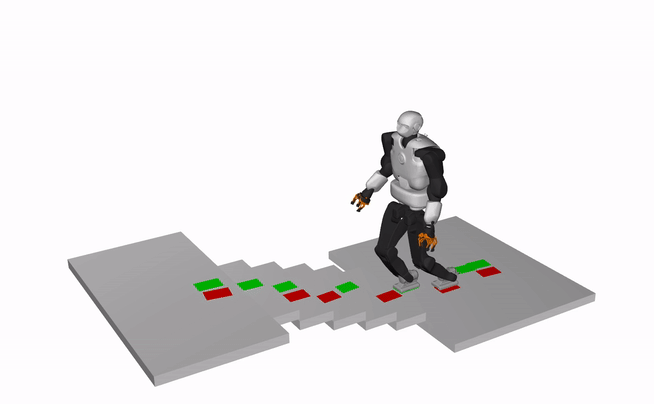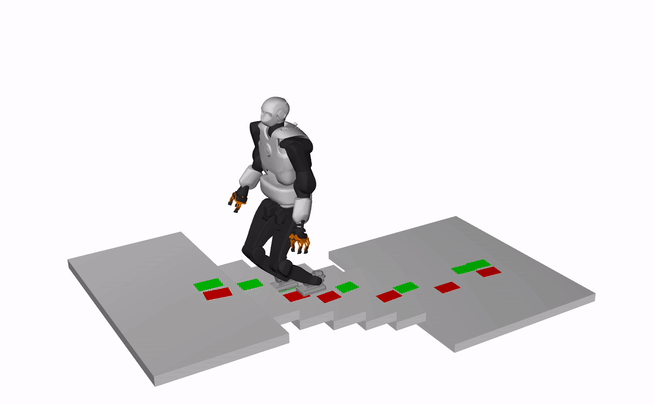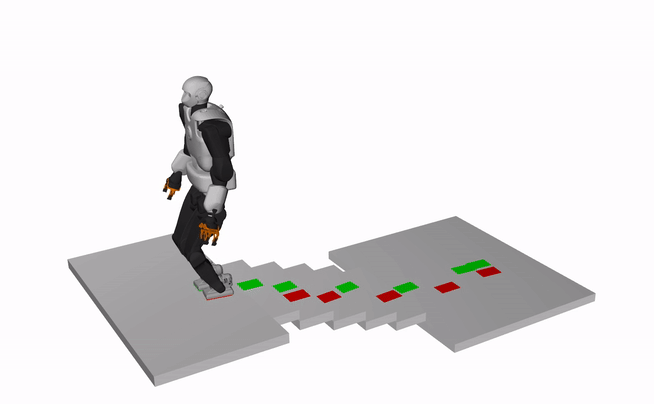
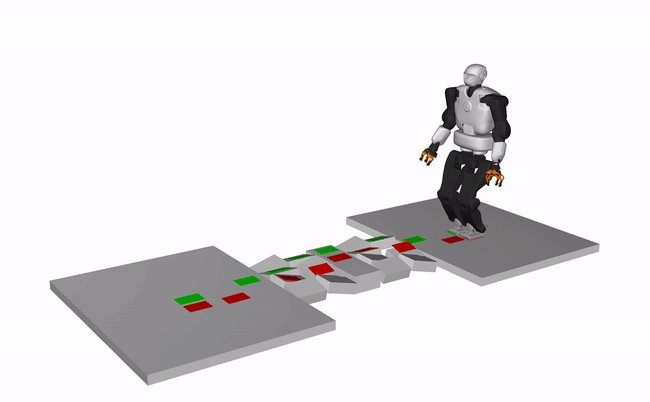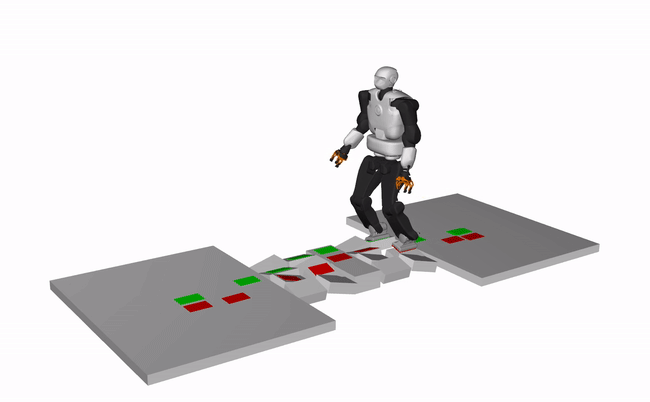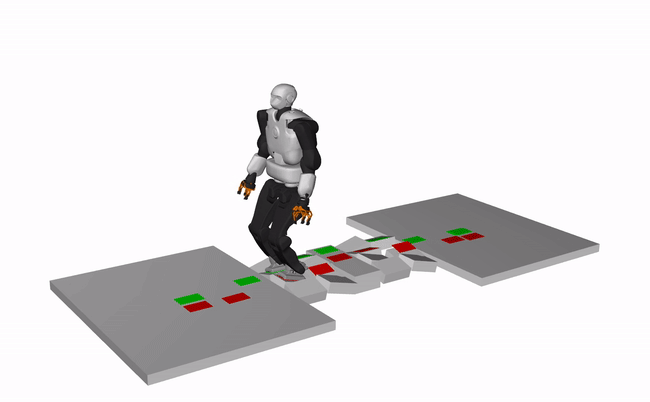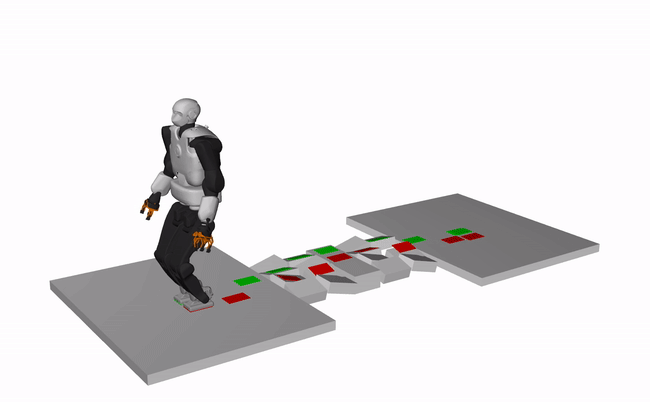
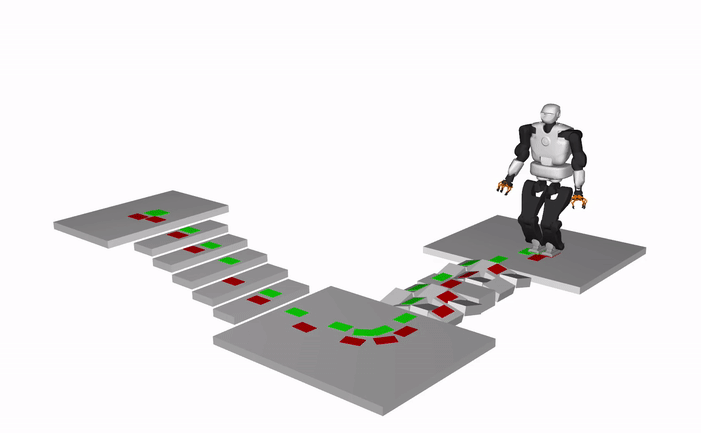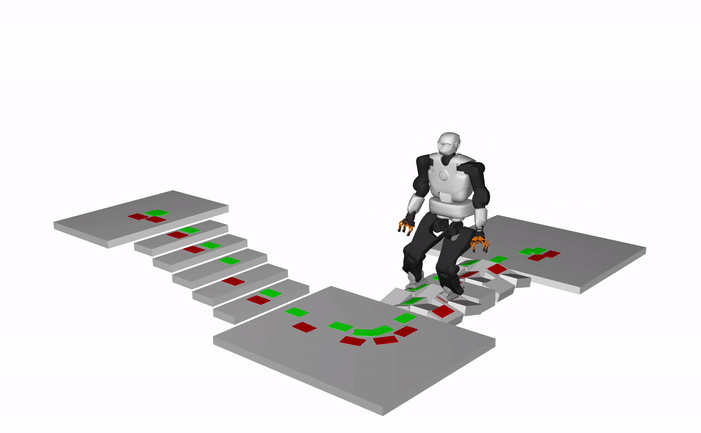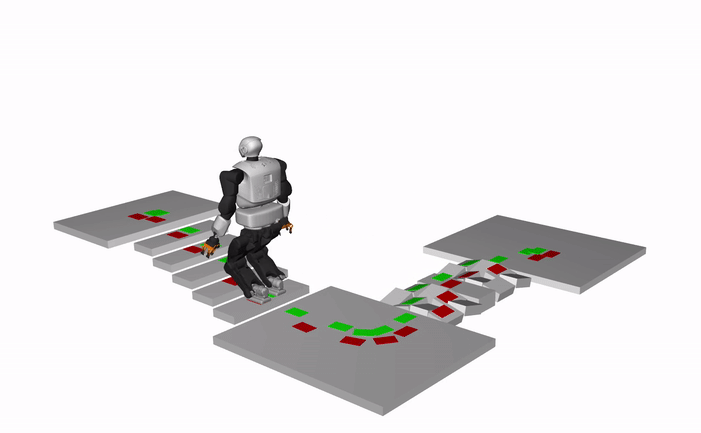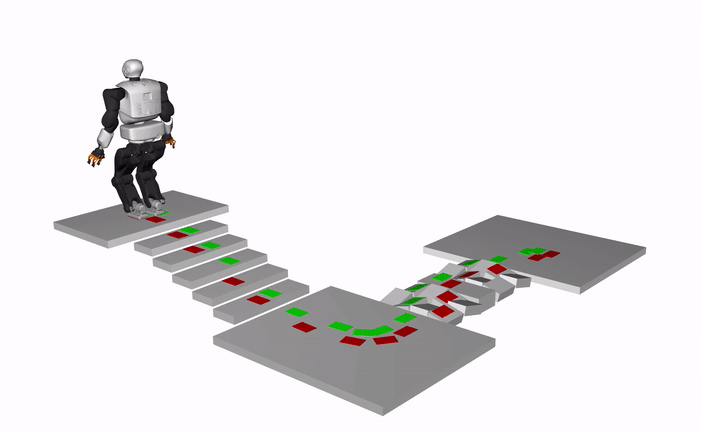
Quadruped, ANYMAL (X3 speed)

Bibtex
IEEE RA-L 2021, "Solving Footstep Planning as a Feasibility Problem Using L1-Norm Minimization":
@ARTICLE{9454381,
author={Song, Daeun and Fernbach, Pierre and Flayols, Thomas and Del Prete, Andrea and Mansard, Nicolas and Tonneau, Steve and Kim, Young J.},
journal={IEEE Robotics and Automation Letters},
title={Solving Footstep Planning as a Feasibility Problem Using L1-Norm Minimization},
year={2021},
volume={6},
number={3},
pages={5961-5968},
doi={10.1109/LRA.2021.3088797}}
}IEEE ICRA 2020, "SL1M: Sparse L1-norm Minimization for contact planning on uneven terrain":
@INPROCEEDINGS{9197371,
author={S. {Tonneau} and D. {Song} and P. {Fernbach} and N. {Mansard} and M. {Taïx} and A. {Del Prete}},
booktitle={2020 IEEE International Conference on Robotics and Automation (ICRA)},
title={SL1M: Sparse L1-norm Minimization for contact planning on uneven terrain},
year={2020},
volume={},
number={},
pages={6604-6610},
doi={10.1109/ICRA40945.2020.9197371}}
}Contact
Ewha Computer Graphics Lab
Department of Computer Science & Engineering, Ewha Womans University
📍 52, Ewhayeodae-gil, Seodaemun-gu, Seoul, Korea, 03760
📞 +82-2-3277-6798
✉️ Daeun Song1, daeunsong@ewhain.net
✉️ Pierre Fernbach2, pfernbach@laas.fr
✉️ Thomas Flayols2, tflayols@laas.fr
✉️ Andrea Del Prete3, andrea.delprete@unitn.it
✉️ Nicolas Mansard2, nmansard@laas.fr
✉️ Michel Taïx2, Michel.Taix@laas.fr
✉️ Steve Tonneau4, stonneau@ed.ac.uk
✉️ Young J. Kim1, kimy@ewha.ac.kr
1 Ewha Womans University, Korea
2 CNRS, LASS, Toulouse, France
3 University of Trento, Italy
4 University of Edinburgh, U.K