Full-body Animation of Human Locomotion in Reduced Gravity using Physics-based Control

Yun-hyeong Kim¹ , Taesoo Kwon² , Daeun Song¹ , and Young J. Kim¹

¹Ewha Womans University, Seoul, Korea , ²Hanyang University, Seoul, Korea

IEEE Computer Graphics and Applications (CG&A)

[Paper] (17.6MB)

    Abstract

    We propose a new physics-based approach to simulate the full-body animation of human locomotion in a reduced gravity environment, such as the Moon or Mars. As input, our method takes motion-captured human motions under Earth's gravitational condition and builds an inverted-pendulum on cart (IPC) control model, which is analyzed using the motion-captured data. Then, for a given gravity condition, we first estimate the desired velocity as well as stride frequency of our character model using the Froude number, map its control model to the altered gravity and plan footsteps that can match the given environmental condition. Using our technique, we can generate stable and robust human gaits in reduced gravity including different gait characteristics. We also compare our results to a known, analytical gait model in the biomechanical literature for reduced gravity, and verify that our method matches the results.

    Keywords — Reduced Gravity ‧ Physically-based Bipedal Control ‧ Human Locomotion

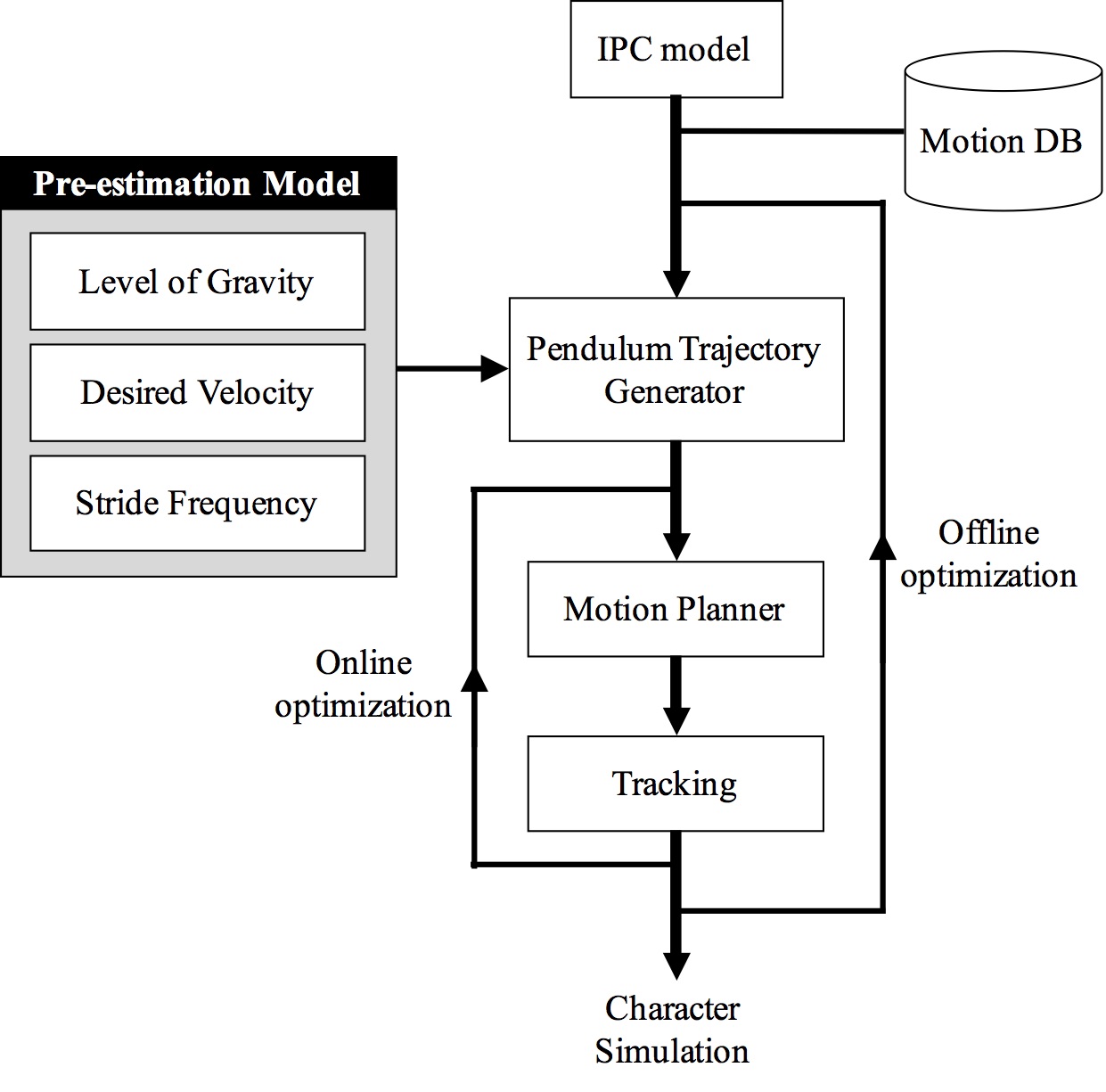
    Our Approach

    Our bipedal simulation is based on an IPC model, that estimates the current state of motion, predicts a short future horizon of the next motion, and maintains the balance of a character. As shown in Fig. 1, our approach consists of four main steps: pre-estimation model, pendulum trajectory generator, motion planner, and tracking. Our system takes a level of gravity as well as a set of motion data captured in Earth's gravity including walking, running and turning. Each motion type is annotated with a state machine; for instance, the walking and turning motions have four states and the running motion has two states.

Fig 1. System diagram

    The pre-estimation model predicts the desired center-of-mass (COM) velocity and stride frequency of the target character in reduced gravity using the Froude number. From the predictive motion, we test if the motion is stable and looks natural. If so, we gradually increase the forward COM velocity and modify the stride frequency accordingly as long as the character moves stably. At every simulation timestep, the pendulum trajectory generator first estimates the state of the IPC model by aligning a captured pose to the current pose of the simulated astronaut. Then, a short future horizon of the pendulum trajectory is planned based on the current estimate of the pendulum state and using the desired velocity determined by our pre-estimation model. Then, the motion planner converts the pendulum trajectory into a desired trajectory of the character motion that includes footstep locations using an inverse kinematics solver. The dynamic motion is synthesized by tracking the desired motion in an online manner. Finally, we generate full-body motion adapted to the surrounding environment. To reproduce a more stable and natural motion, an offline optimization process is executed to find optimal end-effector positions.

    Results

    1. Analysis

    We measure the average COM forward velocity, the stride frequency, and the stride length of our simulated characters, as shown in Table 2, Figs. 2 and 3. The simulated motions show lower velocities and stride-frequencies and shorter stride-lengths in lower gravity except running motion, where we increase its velocity to maximum to create visually-pleasing results.

Table 1. Average COM forward velocity v in m/sec, average stride frequency in 1/sec and average stride length in m in our simulation under different gravity conditions

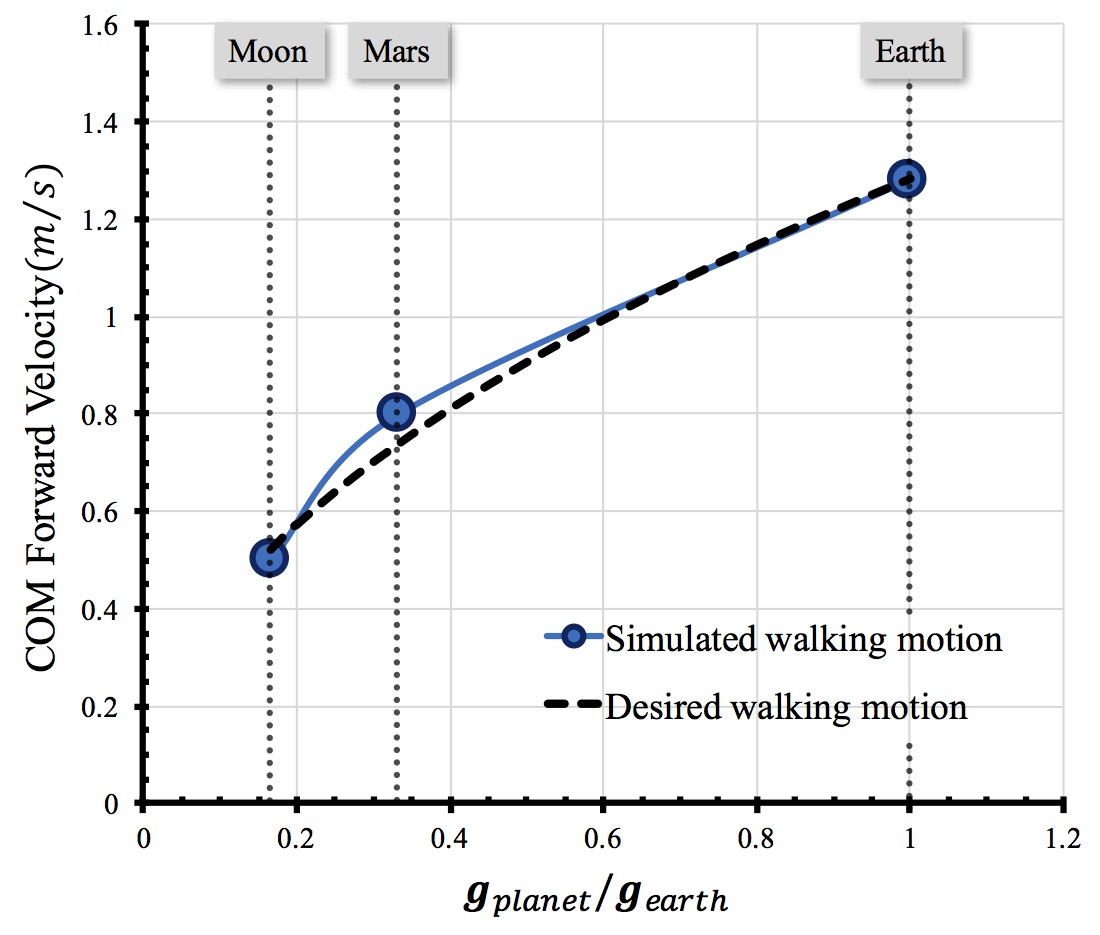
    We analyze the quality of simulation based on the Froude number. Fig. 4 shows graphs for the COM velocity with respect to different gravitational conditions. The used motion here is walking. The dotted line is a curve for the expected COM velocity, estimated from Froude number using v = √ (F_r g h) and the blue curve is a graph of our simulated results interpolated between the Moon's, Earth's and Mars' gravities. The result shows that our simulated results closely resembles the analytical one based on the Froude number.

Fig 4. Comparison against an analytical model using Froude number for walking motion. The x and y axes in the graph denotes the normalized gravity with respect to the Earth's gravity and the COM forward velocity, respectively. The dotted line denotes a curve that is based on the analytical model using v = √ (F_r g h) and the blue line denotes a curve that is based on our simulation results. These curves show a similar pattern of results.

    2. Simulated walking/running/turning motions

    Fig. 5 and the accompanying video show our simulation results including walking, running, and turning under the gravitational conditions of Earth, Mars, and the Moon, respectively. All the simulated motions show stable movements in reduced gravity.

(a) Walking motions

(b) Running motions

(c) Turning motions

Fig. 5 Simulated walking/running/turning motions in gravity of Earth, Mars and the Moon from top to bottom rows, respectively

    3. Quantitative comparison against ground truth

    We quantitatively compare the similarity between our simulated motions and the real video footages of bipedal motions, that were captured by the NASA from the late 1960s to the early 1970s during the Apollo missions. In particular, we use the video clips provided by the NASA and available on the YouTube website (https://youtu.be/S9HdPi9Ikhk? t=54m21s). Here, the real motion starts from 54 minutes 21 seconds and last for 5 seconds in the video clip. We show the sequences of this live footage and of our simulated motion to compare each other in Fig. 6 (a) and (b). We also show the COM trajectories for both simulated motion and real astronaut motion in Fig. 6 (c). According to this experiment, the COM forward velocity, the stride frequency, and the stride length have only about 1~5% relative differences, even considering the fact that the simulation environment is only approximate to the Apollo mission. Our simulated motion visually matches with these ground truth sequences as well. We also show these comparisons in the accompanying video.

(a) The running astronaut motion, annotated with body skeletons in blue and the COM trajectory in red.

(b) Our simulated running motion in the Moon's gravity, annotated with the COM trajectory.

(c) COM height variation with respect to the run distance for the real and simulated motions.

Fig. 6 Simulated walking/running/turning motions in gravity of Earth, Mars and the Moon from top to bottom rows, respectively

    4. Extension to higher gravity

    In order to test the generality of our system, we simulate that the character walks and runs in higher gravities such as Neptune and Jupiter. Neptune and Jupiter's gravity are 1.14 and 2.53 times higher than the Earth's gravity, respectively. In this case, we first set the COM forward velocity properly using our pre-estimation model. As shown in Fig. 10, the character moves stably in higher gravity. In particular, as shown in the accompanying video, in case of walking motion, the higher the level of gravity is, the lower the COM height becomes. In Table. 2, the stride length in Neptune's and Jupiter's cases becomes shorter from 1.44 m to 1.11 m and 1.09 m, and the period of walking motion becomes shorter as well.

Table 2. Average COM forward velocity v in m/sec, average stride frequency in 1/sec and average stride length in m in our simulation under different gravity conditions

(a) Walking motions

(b) Running motions

Fig. 7 Simulated walking/running/turning motions in gravity of Earth, Mars and the Moon from top to bottom rows, respectively

Copyright 2017 Computer Graphics Laboratory

Dept of Computer Science & Engineering

Ewha Womans University, Seoul, Korea

Last update: 2017-03-02

[Privacy Protection]