Abstract

Benchmarking Scenarios

Interactive Continuous Collision Detection for Non-Convex Polyhedra

Xinyu Zhang, Minkyoung Lee and Young J. Kim

Department of Compupter Science & Engineering

Ewha Womans University, Seoul, Korea

{zhangxy,kimy}/AT/ewha.ac.kr

Download

1. Publication in Pacific Graphics 2006 in PDF

(3.8MBytes), Errata (3.5M)

2. Full Video in AVI

(12MBytes)(requires DivX codec)

3. Source Code in C++ (0.9MBytes)

We present a highly interactive, continuous collision detection algorithm for rigid, general polyhedra. Given initial and final configurations of a moving polyhedral model, our algorithm creates a continuous motion with constant translational and angular velocities, interpolating the initial and final configurations of the model. Then, our algorithm reports whether the model under the interpolated motion collides with other rigid polyhedral models in environments, and if it does, the algorithm reports its first time of contact (TOC) with the environment as well as its associated contact features at TOC.

Our algorithm is a generalization of conservative advancement to general polyhedra. In this approach, we calculate the motion bound of a moving polyhedral model and estimate the TOC based on this bound, and advance the model by the current TOC estimate. We iterate this process until the inter-distance between the moving model and the other objects in the environments becomes below a user defined distance threshold. We pose the problem of calculating the motion bound as a linear programming and provide an efficient, novel solution based on the simplex method. Moreover, we also provide a hierarchical advancement technique based on bounding volume traversal tree to generalize the conservative advancement for non-convex models.

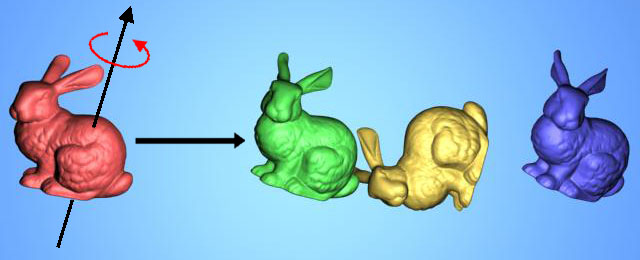
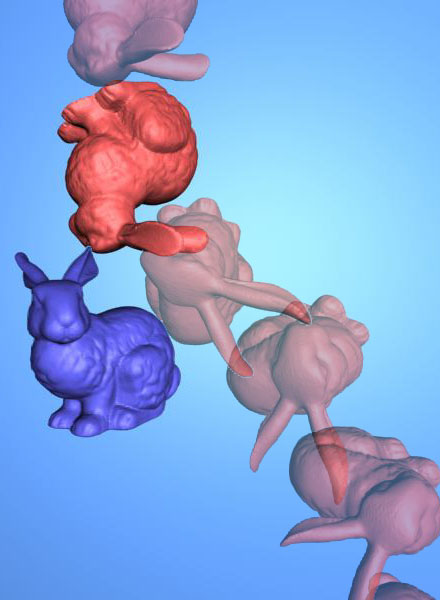
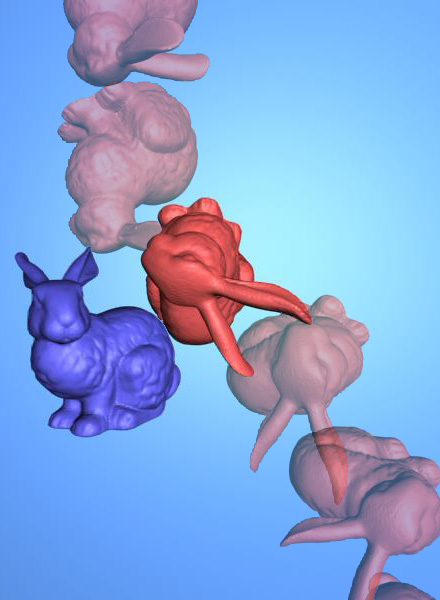
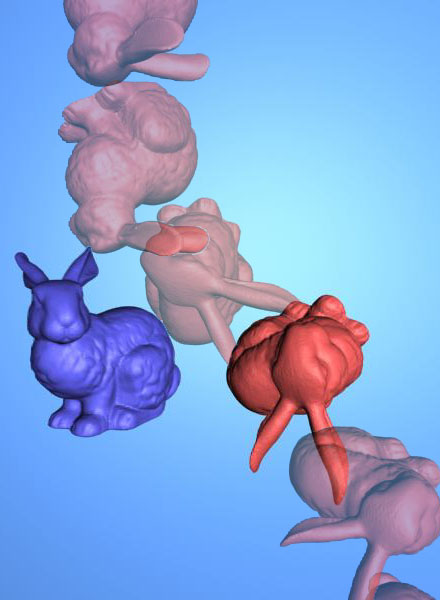
Our algorithm is relatively simple to implement and has very small computational overhead of merely performing discrete collision detection multiple times. We extensively benchmarked our algorithm in different scenarios, and in comparison to other known continuous collision detection algorithm, the performance improvement ranges by a factor of 1.2 ~ 150 depending on benchmarking scenarios. Moreover, our algorithm can perform CCD at 105 ~ 51546 frames per seconds on a 3.6 GHz Pentium 4 PC for complex models consisting of 10K ~ 70K triangles.

Rigid Body Dynamics for Rings

Download Video in AVI (0.9MBytes)

1. Santa vs Thin Board: Given two configurations of q₀, q₁ of a highly non-convex Santa model with 37888 triangles, separated by approximately 5 times the bounding box size of Santa, a board (12 triangles) is initially located below q₀. By varying the position of the board toward q₁, we calculate t_TOC of the Santa model when it tries to reach from q0 to q₁.
In the figure, the red, blue, and green Santas denote the Santa model at configurations, q0, q₁, q(t_TOC), respectively.



		Santa vs Board
Download Video in AVI (2.1MBytes)

2. Bunny vs Bunny: Each bunny consists of 69664 triangles. As shown in the figure, one of the bunny is shot from a random configuration q₀ (red) toward a random configuration q₁ (blue) against a fixed bunny (yellow) with constant translational and angular velocities. We perform this test for more than 200 trials, and between [0,100] steps of the test trial, q₁ has only translation relative to q₀. Afterwards, plus the translational motion, q1 has π/3 rotation around X axis
plus π/3 rotation around Y axis relative to q₀.

Bunny vs Bunny

Download Video in AVI (a) [0,100]

(0.6MBytes), (b) [101, 201]

(0.8MBytes)

3. Torusknot vs Torusknot: It is similar to the bunny vs bunny benchmarking scenario.. However, instead, we use torus-knots in different complexities, 2880, 11520 and 34560 triangles, for benchmarking models.

Torusknot vs Torusknot

Download Video in AVI

(0.6MBytes)

4. Rigid Body Dynamics for Bunnies: Using HAVOK, we perform rigid body dynamics to simulate the falling of a red bunny against a blue one, each consisting of 26K triangles, due to gravity. Each simulation step provides q₀, q₁ of the blue moving bunny, and we plug these into our CCD algorithm and measure the performance. Moreover, in order to create
artificial interpenetration at q1 from this simulation (the simulation itself is collision-free all the time), we slightly modify the q₁ before impact, and thus we can invoke our CCD algorithm to find t_TOC.



Rigid Body Dynamics for Bunnies
Download Video in AVI (1.0MBytes)

5. Rigid Body Dynamics for Rings: We conduct similar dynamics experiments for rings consisting of 10K triangles each.

Dept of Computer Science & Engineering

Ewha Womans University, Seoul, Korea

Last update: Aug 19, 2006

[개인정보보호방침]